释义
1.数据结构和算法解决是“如何让计算机更快时间、更省空间的解决问题”。
2.因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能。
3.分别用时间复杂度和空间复杂度两个概念来描述性能问题,二者统称为复杂度。
4.复杂度描述的是算法执行时间(或占用空间)与数据规模的增长关系。
时间、空间复杂度分析:粗略地估计算法的执行效率的方法,算法的执行效率就是算法代码执行的时间
原因
1.和性能测试相比,复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点。
2.掌握复杂度分析,将能编写出性能更优的代码,有利于降低系统开发和维护成本。
复杂度分析
大O表示法
1、来源
算法的执行时间与每行代码的执行次数成正比,用T(n) = O(f(n))表示,其中T(n)表示算法执行总时间,f(n)表示每行代码执行总次数,而n往往表示数据的规模。
2、特点
以时间复杂度为例,由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势,所以常量阶、低阶以及系数实际上对这种增长趋势不产生决定性影响,所以在做时间复杂度分析时忽略这些项。
复杂度分析法则
1)单段代码看高频:比如循环。
2)多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
3)嵌套代码求乘积:比如递归、多重循环等
4)多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
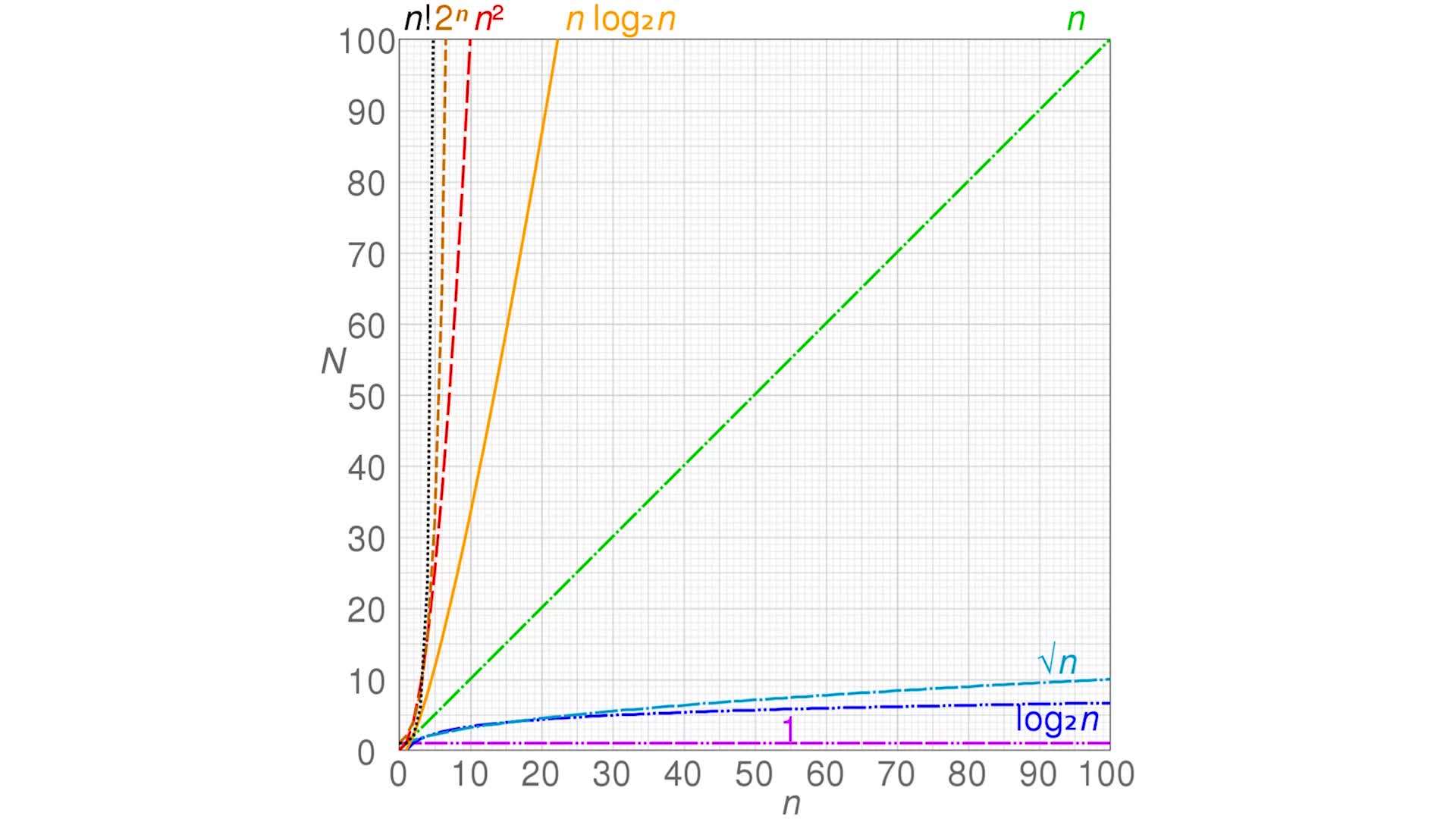
常用的复杂度级别

多项式阶:随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括:
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n2)(平方阶)、 O(n3)(立方阶)
非多项式阶:随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括:
O(2n)(指数阶)、O(n!)(阶乘阶)
示例
假设每行代码执行的时间都一样,为 unit_time。
1、O(n)
int cal(int n) {
int sum = 0; // 1
int i = 1; // 1
for (; i <= n; ++i) { // n
sum = sum + i; // n
}
return sum;
}
所有代码的执行时间为(2n+2)*unit_time
T(n) = O(2n+2)
当 n 很大时,你可以把它想象成 10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了,用大 O 表示法表示,就可以记为:T(n) = O(n);
2、O(n2)
int cal(int n) {
int sum = 0; // 1
int i = 1; // 1
int j = 1; // 1
for (; i <= n; ++i) { // n
j = 1; // n
for (; j <= n; ++j) { // n^2
sum = sum + i * j; // n^2
}
}
}
T(n) = (2n2+2n+3)*unit_time, 即T(n) = O(n2)
3、O(1)
int i = 8;
int j = 6;
int sum = i + j;
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
4、O(logn)、O(nlogn)
i=1;
while (i <= n) {
i = i * 2;
}
从代码中可以看出,变量 i 的值从 1 开始取,每循环一次就乘以 2。当大于 n 时,循环结束。变量 i 的取值就是一个等比数列。通过 2x=n 求解 x(执行次数),x=log2n。时间复杂度就是 O(log2n)。
log3n 等于 log32 * log2n,所以 O(log3n) = O(C * log2n),其中 C=log32 是一个常量。在采用大 O 标记复杂度的时候,可以忽略系数,即 O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于 O(log3n)。在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)。
如果一段代码的时间复杂度为O(logn),循环执行n遍后的时间复杂度就是O(nlogn)。
1> 只关注循环执行次数最多的一段代码
O(n)
int cal(int n) {
int sum = 0;
int i = 1;
for (; i <= n; ++i) { // n
sum = sum + i;
}
return sum;
}
2> 加法法则:总复杂度等于量级最大的那段代码的复杂度
O(n2)
int cal(int n) {
int sum_1 = 0;
int p = 1;
for (; p < 100; ++p) { // 100
sum_1 = sum_1 + p;
}
int sum_2 = 0;
int q = 1;
for (; q < n; ++q) { // n
sum_2 = sum_2 + q;
}
int sum_3 = 0;
int i = 1;
int j = 1;
for (; i <= n; ++i) { // n^2
j = 1;
for (; j <= n; ++j) {
sum_3 = sum_3 + i * j;
}
}
return sum_1 + sum_2 + sum_3;
}
3> 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
O(n2)
int cal(int n) {
int ret = 0;
int i = 1;
for (; i < n; ++i) { // n
ret = ret + f(i);
}
}
int f(int n) {
int sum = 0;
int i = 1;
for (; i < n; ++i) { // n
sum = sum + i;
}
return sum;
}
不同情况下的复杂度
// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) pos = i;
}
return pos;
}
在一个无序的数组(array)中,查找变量 x 出现的位置。如果没有找到,就返回 -1。复杂度是 O(n)。优化如下:
// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
因为,要查找的变量 x 可能出现在数组的任意位置。如果数组中第一个元素正好是要查找的变量 x,那就不需要继续遍历剩下的 n-1 个数据了,那时间复杂度就是 O(1)。
但如果数组中不存在变量 x,那我们就需要把整个数组都遍历一遍,时间复杂度就成了 O(n)。不同的情况下,这段代码的时间复杂度是不一样的。
最好情况时间复杂度(best case time complexity)
在最理想的情况下,执行这段代码的时间复杂度。
最坏情况时间复杂度 (worst case time complexity)
在最糟糕的情况下,执行这段代码的时间复杂度。
平均情况时间复杂度 (average case time complexity)
概率论的方法求加权平均值,即每种情况发生的次数 x 每种情况发生的概率 之和。